统计推断 @ Probability & Statistics Chapter 7
这是 DeGroot, M. H., & Schervish, M. J. (2012). _Probability and statistics_. Pearson Education. 一书的笔记。
7.1 Statistical Inference 统计推断
这一章首首先介绍了灯泡寿命问题。公司想要估计电子元件的failure rate,用未知的参数$\theta$表示,它服从指数分布(gamma分布)。根据大数定律6.2 我们知道独立同分布的样本均值 $\bar{X_i} \xrightarrow{p} \frac{1}{\theta}$ (依概率收敛)。根据Theorem 6.2.5 我们知道给这个式子套一层连续函数也是成立的,即 $1/ \bar{X_i} \xrightarrow{p} \theta$. 所以,我们可以用样本均值的倒数来近似failure rate。
因为我们不可能测量所有元件的寿命,参数$\theta$只能是hypothetically observable的。
接下来定义了统计模型和统计推断(statistical inference)。统计推断的例子:
- 构造一个随机变量$\mathbf{Y}$ 使得 $\text{Pr}(\mathbf{Y} \ge \theta | \theta)=0.9$。 这个RV $\mathbf{Y}$ 可以是观测到的一系列样本$X_1,…,X_m$的函数。
- 在观测到一系列样本$X_1,…,X_m$后,我们有多大把握认为$\theta \le 0.4$。
后面提了下模型参数和参数空间。接着定义了统计量(statistic):是样本$X_1,…,X_n$的实值函数$T=r(X_1,…,X_n)$,例如样本均值$\bar{X_i}$和样本最大值$\max (X_1,…,X_n)$.
7.2 先验 & 后验
先验分布就是在做出观测之前,我们已知或假定参数$\theta$在参数空间$\Omega$上的可能分布。
e.g. 灯泡寿命为指数分布,其损坏率$\theta$假定其先验分布为Gamma分布。
灯泡的损坏率$\theta$服从Gamma分布,它的概率密度为
注意这里会被绕晕:先验概率分布是theta的函数,刻画了theta取各个值的可能性的密度。一般好像RV会用大写$X$,而p.d.f.会用小写$f(x)$?
然后介绍了后文model样本分布的一个notation,即$f_m(\mathbf{x}|\theta)=f(x_1|\theta)…f(x_m|\theta)$。这里,它反过来model了给定$\theta$条件下$X_1,…,X_m$的分布,每个观察值$X_i$都是在给定theta时条件独立同分布(conditional i.i.d.) 的,这时我们可以说$X_1,…,X_m$构成了概率密度函数$f(x|\theta)$的一组随机样本(form a random sample)。
Sensitivity Analysis是分析不同的Prior产生的Posterior有多大程度的不同。这里有一个fun fact是如果实验观测数据足够大,那么不同的先验对试验结果的影响是微乎其微的。这提示我们不必过于纠结怎么挑选先验 (experimenters might be less inclined to spend time specifying a prior distribution if it is not going to matter much),但如果不选择先验的话,就没法计算后验概率了。
后验分布是给定一组样本下的条件概率。The conditional distribution of θ given $X_1, . . . , X_n$ is called the posterior distribution of θ, typically denoted as $\xi(\theta|x_1,…,x_n)$.
与后验分布相关的最重要的东西就是贝叶斯定理了,在随机样本的形势下,贝叶斯定义可以表述为
其中$g_n(\mathbf{x})$为样本的联合概率分布(可由分数线上面部分对$\theta$积分,求得样本$\mathbf{x}$的边际分布得到),整个式子即后验=先验x似然 / 证据 ($\text{Posterior} = \frac{\text{Likelihood}\times \text{Prior}}{\text{Evidence}}$,似然刻画了由先验到后验结果的可能性,证据则是各种结果的出现的可能性)
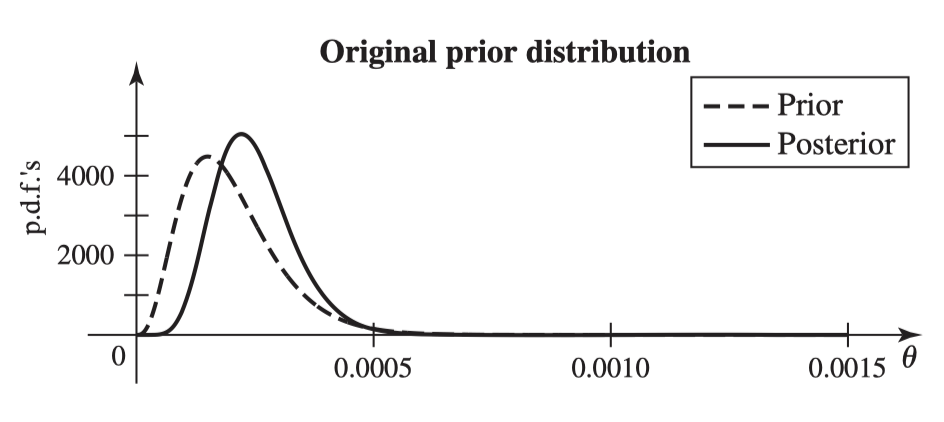
$e.g.$ 这节例子为对之前先验分布为Gamma的灯泡损坏率求后验。
- 似然$f(x|\theta)$为给定theta下每个样本$x_i$的条件概率密度,由于灯泡寿命为指数分布,$f(x|\theta)=\theta e^{-\theta x}$
- evidence是样本的联合概率分布,$g_n(\mathbf{x})=\int^{\infty}_0 f_n(\mathbf{x}|\theta)\xi (\theta) \text{d}x$
- 最后的后验概率为 $\xi(\theta|\mathbf{x})=\frac{(\sum^n_{i=1} x_i+20000)^{n+4}}{\Gamma (n+4)}e^{-(\sum^n_{i=1} x_i+20000)\theta}$ ,是一个关于$\theta$的函数,其中样本$x_i$通过观察得到,视为已知的量。
- 图像上的改变: